The question of how floor standards are defined is one that – to all heads, but particularly those who might be at risk of not meeting them – is obviously of great importance.
And there are clearly numerous ways in which a floor standard could be defined. (We leave to one side the question of whether floor standards are necessary.)
The new Key Stage 4 (KS4) floor standard attempts to identify schools where pupils tend to achieve lower outcomes than pupils with similar Key Stage 2 prior attainment.
From 2015/16, the floor standard has been defined as an average Progress 8 score of -0.5. This replaces the previous floor standard based on achieving five or more A*-C grades at GCSE including English and maths, and expected progress in English and maths.
Professor Simon Burgess and I were involved in developing P8, and, while our brief was mostly limited to a resolving a technical issue around ensuring the measure wasn’t biased in favour of pupils with higher levels of prior attainment, we did give an opinion on how we thought a P8 floor standard could be defined.
Accounting for variability
Schools are particularly worried about pupils who, perhaps for reasons of illness or other unforeseeable circumstances, score no points under Attainment 8, which forms the basis for P8 calculations.
If a pupil with high prior attainment is affected in such a way then his or her P8 score would be large and negative, and potentially exert a relatively large influence on the school’s average P8 score. Tom Sherrington has blogged about this recently.
And, even if we’re not thinking about pupils getting absolutely no points, some groups of children’s results are more variable than others.
As the chart below shows, our calculations suggest the standard deviation in P8 scores differs quite a lot across the prior attainment groups, with less variability in KS4 outcomes among pupils with higher levels of prior attainment.
Standard deviation of Progress 8 scores by KS2 prior attainment band
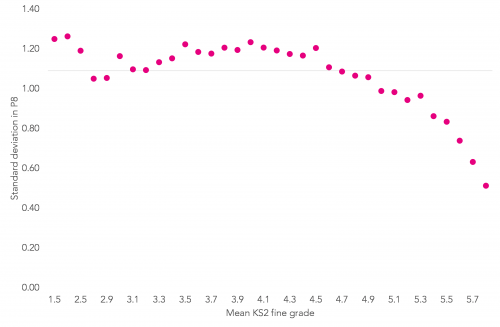
We considered two floor standard approaches that would take account of this kind of variability.
The first was to define a “cause for concern” threshold for each prior attainment group, and calculate the percentage of pupils who fall below their threshold. Such a threshold could be set at, say, half a standard deviation below the mean for their prior attainment group. This method would greatly reduce the effect of individual pupils on summary school measures.
The second approach we considered but did not pursue was more straightforward, and would have involved simply ignoring the top and bottom five per cent of P8 scores when calculating a school’s average. We discounted this idea, though, as it would have offered perverse incentives to effectively write off five per cent of pupils.
What difference does it make?
In the end, the Department for Education (DfE) chose to adopt an average P8 score of -0.5 as the floor standard. But how different are the results, when compared to our cause for concern approach?
From our analysis of the National Pupil Database, we think that, had P8 been applied in 2014/2015, 321 schools would have fallen below the floor of -0.5.
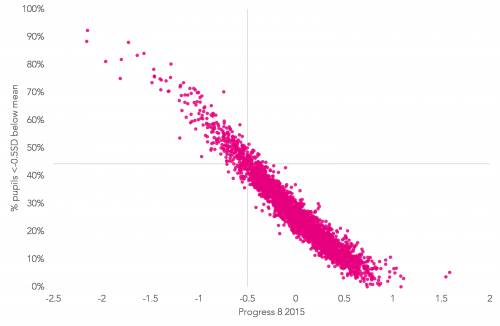
We then rank schools based on the total percentage of pupils who fell more than half a standard deviation below the mean for their prior attainment group. Setting this percentage at 44.25 per cent would have given 321 schools – the same number we think would have been recorded as being under the floor standard that the DfE has gone with.
In the chart below we compare the P8 floor of -0.5 with our alternative floor. There is clearly a high level of correlation.
However, 44 different schools would have fallen below the alternative floor (likewise, 44 schools that we think would have been below the DfE’s floor standard would have been above this alternative floor).
This might not seem a huge number but it would make quite a difference to those schools.
Progress 8 scores versus ’cause for concern’ percentage, by school
Finally, what about the option of removing the highest and lowest scoring five per cent of pupils from the P8 calculation for each school?
Just seven of the 321 schools below the floor based on all pupils would rise above it once this approach is followed. At the same time, though, we think another 11 schools would have fallen below the floor standard.
So, while outliers do have some effect on individual schools’ scores, they don’t appear to make much difference as far as floor standards are concerned.


Can progress 8 data be used to compare classes in a subject within a GCSE subject or between subjects in the same school?
Hi Andy. Not really. I suppose you could look at English and maths though I suspect it would tell you more about levels of motivation in each class (or set) than anything else.
Thanks for the reply.
Is there a straight forward way for a school to compare the quality of teaching (exam outcomes) between classes in a subject or between subject areas. Or does the low number of student i.e. less than 25 in each class mean any measure such as FFT20 are not accurate enough for meaningful conclusions?